Balanced Binary Search Tree (AVL)

AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi (height) / level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dari BST dapat dipersingkat dan disederhanakan. 

Sama Seperti BST , AVL Mempunyai 2 Operasi yaitu : Insertion , dan Deletion
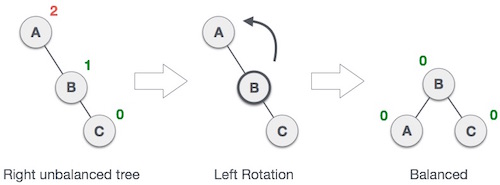
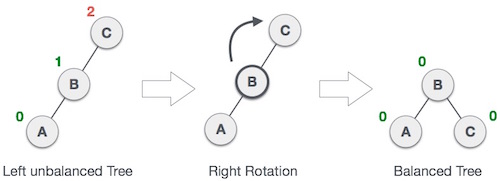
Namun Perbedaan nya Saat selesai Menginsert maupun mendelete seperti biasa , harus di Rotate untuk menyeimbangkan Tree nya.
dalam AVL terdapat 2 jenis Rotation yaitu,
Single Rotation -> Rotation Left,dan  Rotation Right.

Double Rotation -> Rotation Left Right , dan Rotation Right Left.



Cara Menentukan Height dan Balance Factor :
Height :
- Jika node/root tidak memiliki subtree heightnya =0
- Jika node adalah leaf , height =1
- Jika internal node,maka height = height tertinggi dari anaknya dan +1

Balance factor :
-> Selisih Height Anak Kiri - Selisih Height Anak Kanan
-> Jika tidak punya anak , maka dianggap 0
Contoh  Lainnya Sebagai Refrensi Tambahan:

B-Tree

Pada B-Tree dikenal istilah Order. Order menentukan Julah maksimum / minimum anak yang dimiliki oleh setiap node. AVL (Balanced Binary Search Tree ) , RBT (Red Black Tree ) dan 2-3 Tree merupakan salah satu B-Tree berorder 3. Itu sebabnya setiap nodenya memiliki batasan anak , dengan minimal 2 anak dan maksimal 3 anak.

B-Tree adalah pohon seimbang yang dioptimalkan untuk situasi saat sebagian atau seluruh pohon harus dipertahankan dalam penyimpanan sekunder seperti disk magnetik.


Aturan :
1. Setiap Node (Kecuali Leaf) memiliki anak paling banyak x anak
2. Setiap Node (kecuali root) memiliki anak paling sedikit x/2 anak
3. Root memiliki anak minimal 2  (Selama root bukan leaf).
4. Jika Node non-leaf memiliki y anak , maka jumlah data yang tersimpan dalan Node y-1.
5. Data yang tersimpan pada Node harus terurut secara inorder.
6. Semua leaf berada pada level(height) yang sama , level(height) terbawah.

Operasi Pada B-Tree Terdapat : Searching , Insertion , dan Deletion

Kegunaan B-Tree :
1. Menjaga data tetap terurut untuk akses sekuensial.
2. Menggunakan indeks hierarki untuk menimalisir akses ke media penyimpanan.
3. Menggunakan blok penuh-parsial untuk mempercepat penambahan dan penghapusan data.
4. Indeks disesuaikan secara elegan menggunakan algoritma rekursif,
5. Meminimalisir proses yang terbuang dengan memastikan semua simpul setidaknya setengah Penuh.


Daftar Pustaka :
http://suciantinovi.blogspot.com/2014/05/balanced-binary-tree-and-2-3-tree.html
https://en.wikipedia.org/wiki/AVL_tree
http://dinda-dinho.blogspot.com/2013/06/pengertian-dan-konsep-avl-tree.html
http://knowing012.blogspot.com/2014/03/implementasi-b-tree.html
http://suciantinovi.blogspot.com/2014/05/b-tree-and-heap-deap.html

REVIEW

1. Circular Single Linked List

Circular Linked List merupakan Suatu Linked list dimana node / data terakhir menunjuk ke data pertama. Jadi tidak ada pointer yang menunjuk NULL. 

Circular Single Linked List aalah Circular Linked List yang field pointer nya hanya satu buah saja dan satu arah dan membuat bentuk berputar / berulang .

Sama Seperti Single Linked List pada umum nya. Circular Single Linked List mempunyai fungsi Menambahkan data , Menghapus data , dan Melihat data. Perbedaan nya hanyalah Data/Node Tail selalu menunjuk data/node Head.

2. Doubly Linked List

Double / Doubly Linked List atau biasanya di sebut two-way Linked List adalah sekumpulan node / dat yang terurut linear atau sekuensial .Tidak jauh berbeda dengan Single Linked List yang hanya mempunyai satu pointer yaitu next, Double Linnked list mempunyai dua buah pointer yaitu prev dan next.

Double Linked List terdiri dari 3 Bagian : 

- Bagian data informasi

- Pointer Next yang menunjuk ke Node berikutnya

- Pointer Prev yang menunjuk ke Node sebelumnya

Untuk menentukan Head dari Double Linked List , pointer prev dari Node pertama menunjuk NULL . Sedangkan untuk menentukan Tail,pointer next dari Node terakhir menunjuk NULL.

Untuk membuat Linked List , kita perlu membuat Struct menyimpan Data.

struct node {

  int value;

  node *next,*prev;

}*head,*tail;

Pertama-tama kita harus mengalokasikan node baru / mengalokasikan memori  dan menentukan nilainya.

Untuk mengakses Malloc , kita memerlukan library stdlib.h 

node *newNode(int value) {

  node *curr= (node*)malloc(sizeof(node));

  curr->value=value ;

  curr->next=curr->prev=NULL;

  

  return curr;

   

  }

Kemudian Membuat Fungsi Seperti Menambahkan Data / Push , Mendelete Data/ Pop , dan Melihat Data.

Contoh Menambah Kan Data/Node dari depan / Push Head :

- Jika Tidak Mempunyai Node/Data sama sekali , Langsung membuat Head , tail  , dan curr nya di 1 tempat yang sama.

- Jika Mempunyai Node/Data >= 1 , langsung menambahkan di depan.

Contoh Menghapus Data / Node dari depan / Pop Head:

-Jika Data nya cuman 1 Langsung Membuat NULL data tersebut , kemudian melepaskan data tersebut /Free(Head).

-jika mempunyai Data / Node >1 . Kita buat Variabel Temp di Head , dan Buat si Head nya geser ke data sesudah nya . Kemudian Temp -> next dan Head-> prev harus menunjuk ke NULL . Sesudah itu kita bisa melepaskan si Temp / free(temp).

Contoh Melihat Data / Node dari depan : 

- kita buat variabel Temp di Head , Selama si Temp != NULL , kita bisa meng print Data tersebut  dan menggeser temp ke data selanjutnya, 

3. Circular Doubly Linked List 

Circular Doubly Linked List hampit sama dengan Circular Single Linked List dimana node / data terakhir menunjuk ke data pertama. Jadi tidak ada pointer yang menunjuk NULL. , cuman perpedaan nya adalah setiap node mempunyai 2 pointer ( next dan prev).

4. Stack And Queue 

1. Stack 

Stack atau tumpukan dapat diartikan suatu kumpulan data yang seolah -olah terlihat seperti ada data yang diletakkan di atas data yang lain. Kaidah utama konsep stack adalah LIFO (Last In First Out) yang artinya data yang terakhir kali di masukkan atau di simpan , maka data tersebut adalah data yang pertama kali di keluarkan . Menggunakan Fungsi PushTail , popTail.

Seperti Contoh : pada Tumpukan Piring .
Piring yang paling atas biasanya di ambil terlebih dahulu. 

2. Queue

Queue atau antrian merupakan stuktur data linear dimana ujung yang 1 ditambah , dan ujung yang lain berkurang. Kaidah utama konsep Queue adalah FIFO ( First In First Out) artinya data yang pertama kali di masukkan / disimpan ,  data tersebut adalah data yang pertama kali di keluarkan .Menggunakan Fungsi PushHead , PopHead.

Seperti Contoh : Pada Antrian
Orang yang pertama kali mengantri dan sesudah di layani dia akan keluar pertama kali.

Hashing  and Hash Table , Trees and Binary Tree

Tugas Utama dari Hashing adalah untuk memastikan integritas(keutuhan).Contohnya kita mempunyai sebuah file . Dengan di-Hashing kita akan mendapatkan nilai tertentu sebagai bagian integritas file tersebut.Apabila file itu dirubah, maka nilainya tidak akan sama lagi dengan Hashing pertama.

Nah.. kan udah pada tau kira - kira hashing itu apa , Sekarang Apa sih itu Hash Table?

Hash Table adalah sebuah Struktur data yang terdiri atas sebuah tabel dan fungsi yang bertujuan untuk memetakan nilai kunci yang unik untuk setiap baris menjadi angka /hash lokasi record tersebut dalam sebuah tabel .

Keunggulan dari struktur hash table ini adalah waktu aksesnya yang cukup cepat.

Operasi pada Hash Table :

1. Insert -> diberikan sebuah key dan nilai , insert nilai dalam tabel

2. Find -> diberikan sebuah key,temukan nilai yang berhubungan dengan key

3. Remove -> diberikan sebuah key, temukan nilai yang berhubungan dengan key , kemudian hapus nilai tersebut.

4. getIterator -> mengembalikan iterator , yang memeriksa nilai satu demi satu.

Tahap Tahap Membuat Hash Table : 

1. Inisialisasi

2. Menambah Element Baru

3. Menghapus Sebuah element

4. Searching , teknik pencarian pada hash table yaitu mencari nilai hash yang sesuai menggunakan deklarasi sama seperti pada linked list. Jika data tidak

 ditemukan maka menggunakan return NULL .

5. Resizing , Jumlah element pada hash table tidak selalu diketahui ketika terjadi penambahan data.

Collision / Tabrakan

Keterbatasan tabel hash menyebabkan ada dua angka yang jika dimasukkan ke dalam fungsi hash maka menghasilkan nilai yang sama . Hal ini disebut dengan collision

contoh : kita memasukkan angka 6 dan 29

Hash(6) = 6 % 23 = 6;

Hash(29) = 29 %23 =6;

Cara mengatasi Collision / Collision Resolution :

1. Open Addressing (Linear Probing,Quadratic Probing,Double Hashing)

2. Chaining

Biasanya dalam Hash Table kita sering memakai Linear Probing / Chaining,

Contoh pada Linear Probing , Saat kita memiliki String yang sama seperti "bima" dan "bima"

dia akan mengeluarkan output seperti ini

(index).bima

(index).bima

Sedangkan Chaining , ia menggunakan konsep seperti linked List

(index).bima->bima

Tree dan Binary Tree

Binary Tree atau pohon Biner adalah sebuah pohon dalam struktur data yang bersifat hirarkis (hubungan one to many). Tree bisa di definisikan sebagai kumpulan simpul dengan setiap simpul yang mempunyai paling banyak dua anak (anak kanan , anak kiri).

Operasi dalam Binary Tree -> Create , Clear , Find , Update , Delete

Binary Search Tree adalah Tree yang terurut (Ordered Binary Tree). Binary Serach Tree juga sering di sebut dengan Sorted Binary Tree yang berfungsi untuk menyimpan informasi nama atau bilangan yang disimpan di dalam meory . 

Aturan dalam BST :

1. Semua data di bagian kiri sub tree  dari root selalu lebih kecil dari root itu sendiri

2. Semua data di bagian kanan sub tree dari root selalu lebih besar dari root itu sendiri

Binary Search Tree(BST)

Kali ini , kita belajar Binary Search Tree / BST. Kita pertama - tama akan membahas struktur dasar Tree terlebih dahulu . Tree (pohon) adalah salah satu bentuk struktur ata yang menggambarkan hubungan hierarki antar elemen-elemennya(seperti relasi one to many).

Nah... Binary Tree atau pohon biner adalah suatu tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua subtree dan kedua subtree terhebut harus terpisah. Tiap node dalam binary tree boleh memiliki paling banyak 2 child / anak simpul (anak kiri ,anak kanan). Dan saat Menginsert nya dia masih belum tersusun rapi.

Binary Search Tree adalah tree yang terurut (ordered Binary Tree) / Sorted Binary Tree yang berfungsi untuk menyimpan informasi nama atau bilangan yang di simpan di dalam memory. Dengan ini data dibagi menjadi dua dengan mencari titik tengah sebagai patokannya. Binary Tree terdiri dari 1. simpul utama yang disebut dengan istilah root, dan setiap root mempunyai 2 child. 

2. 2 child yang memiliki 1 root yang sama di sebut Sibling , 

3. suatu root yang tidak memiliki child sama sekali di sebut leaf

Data yang tersusun dalam struktur data BST juga dapat dicari dengan mudah dan memiliki rata- rata kompleksitas sebesar O(log n),namun membutuhkan waktu sebesar O(n) pada kondisi terjelek dimana BST tidak berimbang dan membentuk seperti linked list.

2 aturan yang harus di penuhi pada saat data di atur dalam BST :

1. Semua data di bagian kiri sub-tree dari node  selalu lebih kecil dari data dalam node t itu

2. semua data dibagian kanan sub-tree dari node  selalu lebih besar atau sama dengan data dalam node 

Operasi BST : 

-Insertion 

1. Dimulai dari root 

2. Jika x lebih kecil dari key kemudian cek dengan sub-tree sebelah kiri , lakukan pengecekan secara rekursif.

3. Jika x lebih besar dari key kemudian cek dengan sub-tree sebelah kanan ,lakukan pengecekan secara rekursif.

4. Ulangi sampai menemukan node yang kosong untuk memasukkan value 

-Delete

1. Jika value yang ingin dihapus adalah leaf , langsung delete saja

2. Jika value yang akan dihapus mempunyai satu child , hapus nodenya dan gabungkan childnya ke parent value yang dihapus.

3. Jika value yang akan di hapus adalah noode yang mempunyai 2 child , maka cari dari left sub-tree ,kemudian bandingan dengan yang kanan .