Brian Karnadi Japar
2301869891
Hari : Selasa,9/Juni/2020
Kelas : CB01-CL
Lecturer : Ferdinand Ariandy Luwinda (D4522) , Henry Chong (D4460)
2301869891
Hari : Selasa,9/Juni/2020
Kelas : CB01-CL
Lecturer : Ferdinand Ariandy Luwinda (D4522) , Henry Chong (D4460)
Balanced Binary Search Tree (AVL)
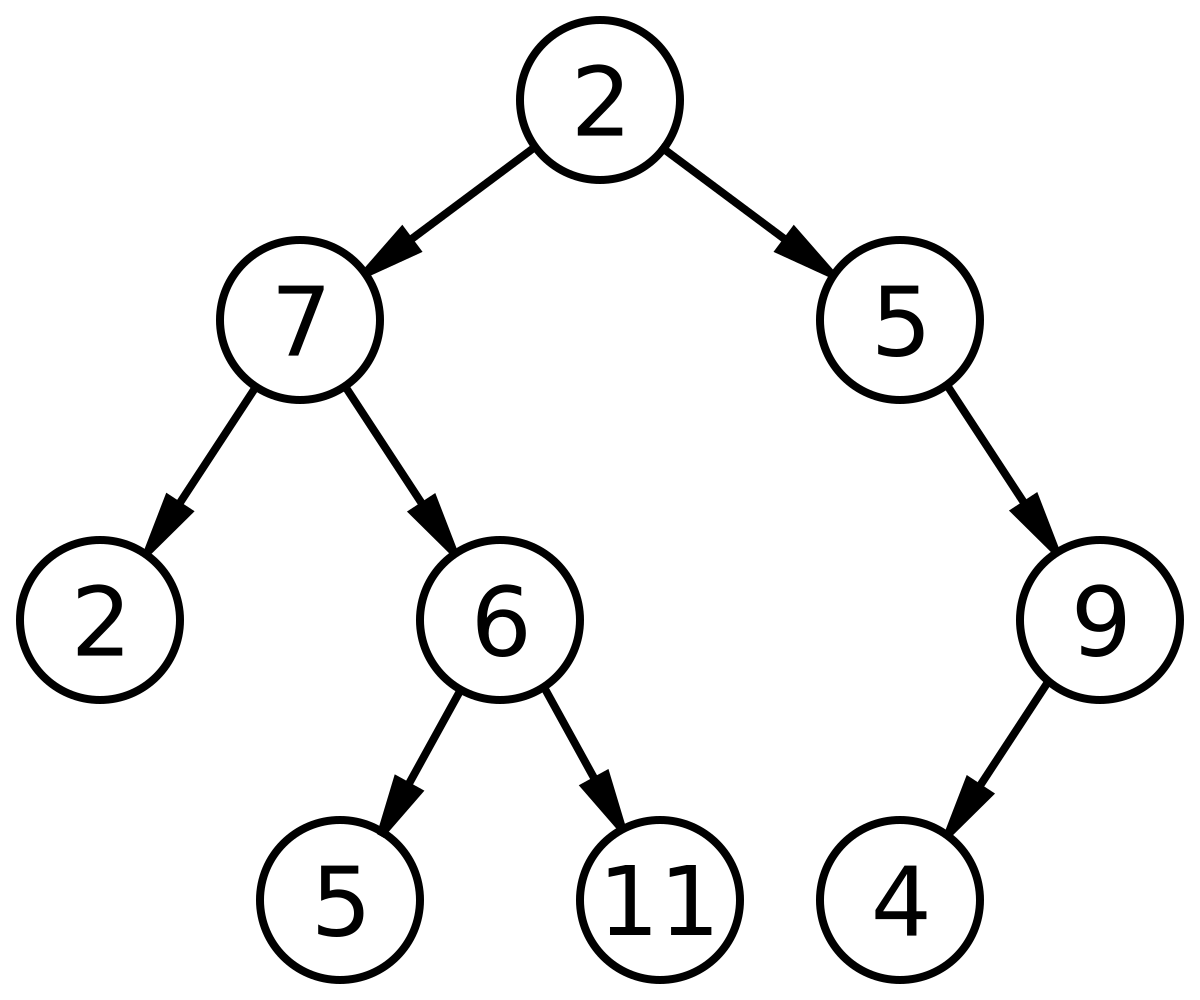
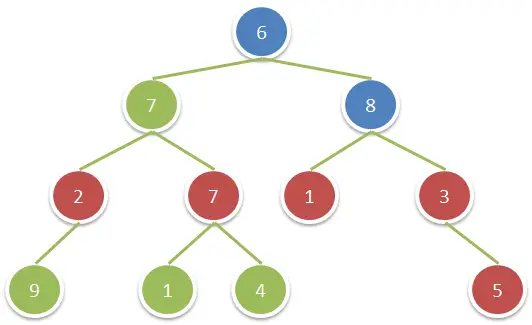
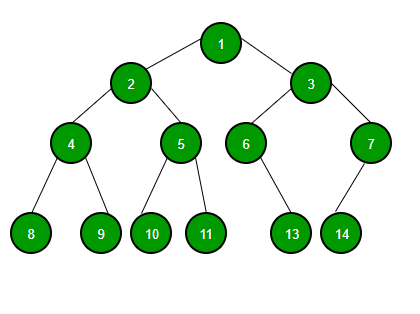
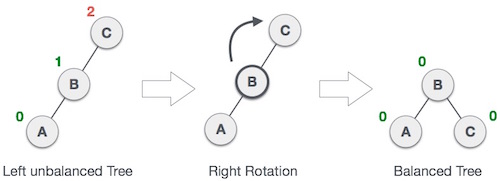
AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi (height) / level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dari BST dapat dipersingkat dan disederhanakan.Sama Seperti BST , AVL Mempunyai 2 Operasi yaitu : Insertion , dan Deletion
Namun Perbedaan nya Saat selesai Menginsert maupun mendelete seperti biasa , harus di Rotate untuk menyeimbangkan Tree nya.
dalam AVL terdapat 2 jenis Rotation yaitu,
Single Rotation -> Rotation Left,dan Rotation Right.

Double Rotation -> Rotation Left Right , dan Rotation Right Left.


Cara Menentukan Height dan Balance Factor :
Height :
- Jika node/root tidak memiliki subtree heightnya =0
- Jika node adalah leaf , height =1
- Jika internal node,maka height = height tertinggi dari anaknya dan +1
Balance factor :
-> Selisih Height Anak Kiri - Selisih Height Anak Kanan
-> Jika tidak punya anak , maka dianggap 0
Contoh Lainnya Sebagai Refrensi Tambahan:
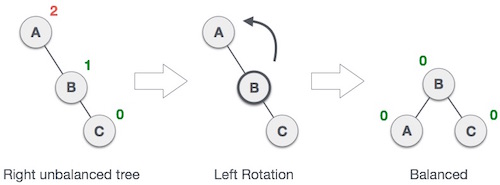

B-Tree
Pada B-Tree dikenal istilah Order. Order menentukan Julah maksimum / minimum anak yang dimiliki oleh setiap node. AVL (Balanced Binary Search Tree ) , RBT (Red Black Tree ) dan 2-3 Tree merupakan salah satu B-Tree berorder 3. Itu sebabnya setiap nodenya memiliki batasan anak , dengan minimal 2 anak dan maksimal 3 anak.B-Tree adalah pohon seimbang yang dioptimalkan untuk situasi saat sebagian atau seluruh pohon harus dipertahankan dalam penyimpanan sekunder seperti disk magnetik.

Aturan :
1. Setiap Node (Kecuali Leaf) memiliki anak paling banyak x anak
2. Setiap Node (kecuali root) memiliki anak paling sedikit x/2 anak
3. Root memiliki anak minimal 2 (Selama root bukan leaf).
4. Jika Node non-leaf memiliki y anak , maka jumlah data yang tersimpan dalan Node y-1.
5. Data yang tersimpan pada Node harus terurut secara inorder.
6. Semua leaf berada pada level(height) yang sama , level(height) terbawah.
Operasi Pada B-Tree Terdapat : Searching , Insertion , dan Deletion
Kegunaan B-Tree :
1. Menjaga data tetap terurut untuk akses sekuensial.
2. Menggunakan indeks hierarki untuk menimalisir akses ke media penyimpanan.
3. Menggunakan blok penuh-parsial untuk mempercepat penambahan dan penghapusan data.
4. Indeks disesuaikan secara elegan menggunakan algoritma rekursif,
5. Meminimalisir proses yang terbuang dengan memastikan semua simpul setidaknya setengah Penuh.
HEAP
Heap adalah sebuah Tree yang mempunyai ketentuan sebagai berikut :
1. Tree harus complete binary Tree
- Semua level tree mempunyai simpul maksimum kecuali padda level terakhir.
- pada level terakhir, node tersusun dari kiri ke kanan tanpa ada yang di lewati.
2. Perbandingan nilai suatu node dengan nilai node childnya mempunyai ketentuan berdasarkan jenis Heap,diantaranya :
- Max Heap mempunyai ketentuan bahwa nilai suatu node lebih besar atau sama dengan(>=) dari nilai childnya.
- Min Heap mempunyai ketentuan bahwa nilai suatu node lebih kecil atau sama dengan (<=) dari nilai childnya.
Ada 2 Jenis Heap :
1. Min Heap : Node paling kecil adalah root dan semakin kebawah levelnya semakin besar.
2. Max Heap : node paling besar adalah root dan semakin kebawah levelnya semakin kecil.
3. Min-Max Heap : min-heap dan max-heap levelnya saling bergantian pada tree.
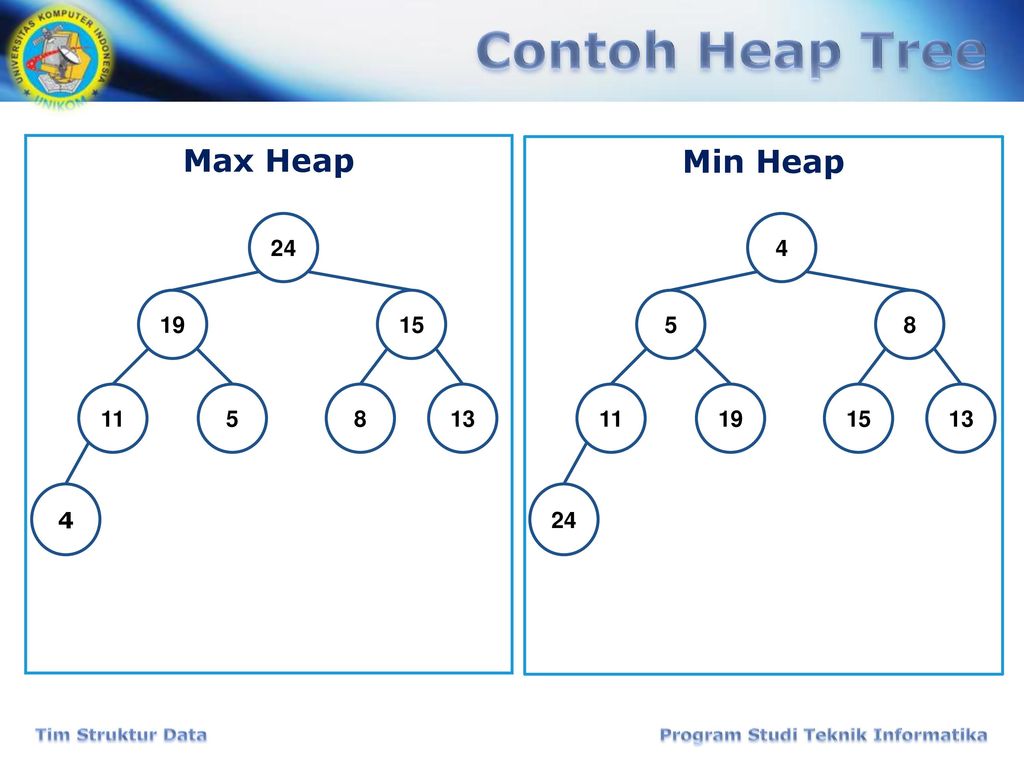 |
| Contoh Max Heap dan Min Heap. |
Heap biasanya diimplementasikan pada array dan indexnya dimulai dari 1, bukan 0.

Cara Mengetahui Lokasi Index parent dan child :
1. Parent(x) = x/2 ,dengan x = index Child
2. Left-Child(x)= 2*x ,dengan x = index parent
3. Right-Child(x)=2*x+1 ,dengan x = index parent.
Operasi pada Heap ada 2 Macam yaitu Insertion dan Deletion.
Insertion
pada heap , saat node baru di masukkan ia akan memenuhi anaknya terlebih dahulu (kiri ke kanan),
Dalam Proses Insert , ada namanya UpHeap / HeapifyUp (Yang artinya kalau node tersebut lebih kecil dia akan naik (Min Heap ) , atau kalau node tersebut besar node tersebut akan naik (Max Heap)).
Insertion MinHeap
1. Insert node baru pada index selanjutnya (setelah index terakhir).
2. Lakukan UpHeap,yaitu membandingkan key dengan parentnya . Jika node parent > key, maka di swap. Jika tidak maka biarkan saja.
3. Lakukan point ke-2 berulang kali jika setelah diswap masih parent>key. Namun stop jika key sudah berada pada posisi root.
Contoh :
Insert 5


Insertion MaxHeap
1. Insert Node baru(Key) pada index selanjutnya (setelah index terakhir)
2. Lakukan UpHeap, yaitu membandingkan key dengan parentnya . Jika node parent < key, maka di swap. Jika tidak maka biarkan saja.
3. Lakukan point ke-2 berulang kali jika setelah diswap masih parent<key. Namun stop jika key sudah berada pada posisi root.
Contoh:
Insert 15

DELETION
Kebalikan dari proses insert di dalam deletion ada namanya DownHeap / HeapifyDown
Min Heap Deletion
Aturan :
- Operasi delete hanya terjadi pada rootnya saja.
- gantikan elemen yang di delete dengan node yang berada pada index terakhir.
- lakukan downHeap, yaitu membandingan dengan salah satu childnya yang terkecil. Jika node tersebut > child terkecil , maka swap.
- Lakukan point ke-3 berkali kali jika setelah diswap node tersebut masih memiliki anak. Namun Stop jika node sudah dalam posisi leaf atau node tersebut < child terkecilnya.
Contoh:
Delete 7


Max Heeap Deletion
Aturan :
- Operasi delete hanya terjadi pada rootnya saja.
- gantikan elemen yang di delete dengan node yang berada pada index terakhir.
- lakukan downHeap, yaitu membandingan dengan salah satu childnya yang terbesar. Jika node tersebut < child terbesar , maka swap.
- Lakukan point ke-3 berkali kali jika setelah diswap node tersebut masih memiliki anak. Namun Stop jika node sudah dalam posisi leaf atau node tersebut > child terbesarnya.
Min-Max Heap
Min-Max Heap adalah penggabungan dari min-Heap dan Max-Heap. Dimana pada tree ini kita dapat mendapatkan 1 angka terkecil dan 2 angka terbesar. Namun sayangnya , angka terbesar tersebut salah satunya memang terbesar tetapi satunya lagi belum pasti nilai terbesar keduanya.
Contoh:

Level pertama pada Min-Max heap addalah min level dibawhanya max level. Nilai terkecil pada tree terletak pada rootnya, sedangkan 2 nilai terbesarnya adalah anak dari rootnya.
Insert Min-Max Heap
1. Insert node baru(key) pada index selanjutnya (setelah index terakhir)
2. Jika key terletak pada level min:bandingan dengan parentnya
- Jika parent < key maka swap dan UpHeap Max dari parentnya(Bandingkan dengan grand parentnya dari posisi key setelah di swap)
- Jika parent > key, Upheap Min dari posisi key(Bandingkan dengan GrandParentnya dari posisi key).
3. Jika key terletak pada level max :
- Jika parent > key maka swap dan UpHeap Min dari parentnya (bandingkan dengan GrandParentnya dari posisi key setelah di swap).
- Jika parent < key, UpHeap Max dari posisi key(Bandingkan dengan grandParentnya dari posisi key).
Deleteion Min-Max Heap
ada 2 jenis delete, yaitu delete min , dan delete max
1. Delete min , menghapus node terkecil, yaitu root
2. Delete Max,Menghapus node terbesar, yaitu salah satu dari anak root
Heap Sort
Min Sort -> Ascending
Max Sort -> Descending
Jadi jika kita mempunyai angka
10,15,12,18,20,17,28,21,35,22
Kita kalau mau mengurutkannya dengan cara di tampung.
Caranya :
1 . Menampung Root an hapus root tersebut sementara
2. Lakukan swap seperti biasa .
3. lakukan cara yang di atas sampai semua angka tertampung
4. Kemudian Insert seperti biasa.
TRIES
Tries atau prefix Tree adalah suatu pohon struktur data yang terurut yang menyimpan data array, biasanya String. Kata tries diambil dari kata RETRIEVAL, karena tries dapat menemukan katatunggal dalam kamus hanya dengan awalan katanya saja.
Tries sudah diterapkan ke banyak hal dalam kehidupan sehari-hari,contohnya pada web browser. Suatu web browser dapat mengira atau mensugestikan kata-kata yang mungkin kita maksud saat kita mengetik huruf pertamanya saja (autocomplete).
Contoh :

Kemudian selain itu juga pada spell checker,spell checker dapat mengetahui spelling kata yang tepat saat kita melakukan kesalahan dalam pengetikan.
Tries adalah suatu tree dimana setiap vertex/Pathnya menggambarkan suatu kata,rootnya kosong.

Daftar Pustaka :
http://suciantinovi.blogspot.com/2014/05/balanced-binary-tree-and-2-3-tree.html
https://en.wikipedia.org/wiki/AVL_tree
http://dinda-dinho.blogspot.com/2013/06/pengertian-dan-konsep-avl-tree.html
http://knowing012.blogspot.com/2014/03/implementasi-b-tree.html
http://suciantinovi.blogspot.com/2014/05/b-tree-and-heap-deap.html
http://suciantinovi.blogspot.com/2014/05/balanced-binary-tree-and-2-3-tree.html
https://en.wikipedia.org/wiki/AVL_tree
http://dinda-dinho.blogspot.com/2013/06/pengertian-dan-konsep-avl-tree.html
http://knowing012.blogspot.com/2014/03/implementasi-b-tree.html
http://suciantinovi.blogspot.com/2014/05/b-tree-and-heap-deap.html